Total Quality Management

A Burrito Rule Consultancy Training Project

Total quality management (TQM) consists of organisation-wide efforts to install and make permanent a climate in which an organisation continuously improves its ability to deliver high-quality products and services to customers. While there is no widely agreed-upon approach, TQM efforts typically draw heavily on the previously developed tools and techniques of quality control.

This document is meant to introduce the concept of TQM and all submodules that it encapsulates. It is also meant as a reference for TQM teaching. This document is split into sections which each cover a core aspect of TQM. At the end of the document is a quiz that should be used to test your understanding of TQM.

What follows is a video that introduces TQM in the context of a sandwich production line.

 

Table of Contents

Definition of Quality

Quality is a somewhat abstract, subjective concept with people interpreting it differently. Like the 'theory of relativity', quality is expressed as a relative concept and can be different things to different people. For example:

"A Rolls Royce car is a quality car for certain customers whereas a VW Beatle can be quality car for other customers."

Therefore, consumers may tend to focus on the eventual specification quality of a product/service, or how it compares with the competing companies in the marketplace. However, producers might measure the conformance quality, or the degree to which the product/service was produced correctly. The producer of a product may focus on process variation minimisation, to achieve uniformity amongst and between batches.

Five discrete and interrelated definitions of quality are listed below (Garvin, 1988):

Six Sigma

Six sigma represents a set of techniques and tools for implementing process improvement. This improvement is achieved through identifying and subsequently removing the causes of defects, thus minimising variability in manufacturing and business processes. A six sigma process is one in which 99.99966% of all opportunities to produce some feature or part are statistically expected to be free of defects (3.4 defective features per million opportunities). A defect in this sense can be defined as any variation of a required characteristic of the product for its parts, which is far enough removed from its nominal value to prevent the product from fulfilling the physical and functional requirements of the customer.

Normal distribution curves (Figure 1) are symmetrical about the mean value (μ), with the total area under the curve equating to one. If a process is classified as 3 sigma, 99.7% of outputs are defect free. Mean is the central tendency of the process, or the average of all values within the population. The standard deviation (σ) is a measure of dispersion or variability.

Figure 1: A normal distribution curve, with the standard deviations from the mean marked.

The upper specification limit (USL) and the lower specification limit (LSL) set permissible limits for the process variation. For example, the USL and LSL of a process may be set at 3σ and -3σ, thus yielding a process which is 99.7% defect free. USL represents a value designating an upper limit above which the process or characteristic performance is unacceptable. In the converse case, the LSL represents a value designating a lower limit, below which the process or characteristic performance is unacceptable.

The relationship between yield, variability and specification limits is that essentially the specification limits provide the permissible process variations. Minimising variability therefore inherently leads to a better yield, as the probability of defects occurring is substantially mitigated. Cp and Cpk represent metrics of process quality. Cp is a measure of how capable the process is of producing the required process characteristic. Cp is known as the capability index, or design margin, and is calculated using the following equation:

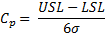
Cpk is a measure of actual performance which takes the operating mean into account. Cpk is equal to Cp when the process mean is equal to the target, or nominal value. Cpk accounts for the process mean not hitting the target value. The following calculations can be used to determine Cpk.

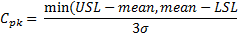
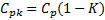
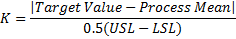
Poisson distributions describes the probability distribution of an event occurring with respect to time, or space. The eventual process yield can be calculated using Poisson's formula as presented below, where dpu is the measured defects per unit.

As an example, if average dpu = 1, the probability of having a device with no defects can be calculated as:

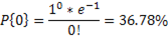
Relationship Between Quality and Reliability

Quality assures the product will work after assembly, whereas reliability relates to the probability that the design will perform its intended function for a designated period of time under specified conditions. Engineering process reliability is the fundamental concept that is meant to anticipate quality failures over the life cycle of a product. Variation of the process output may affect both quality and reliability.

Controlling reliability is much more complex and cannot be controlled by a standard "quality" (Six Sigma) approach, as they need a systems engineering approach. Quality is a snapshot at the start of life and mainly related to control of lower level product specifications and reliability is (as part of systems engineering) more of a system level motion picture of the day-by-day operation for many years. Time zero defects are manufacturing mistakes that escaped quality control, whereas the additional effects that appear over time are 'reliability defects'.

Impact of Quality on Cycle Time and Cost

These three project managment constraints are traditionally represented in what is known as the "Iron Triangle", depicted in Figure 2.

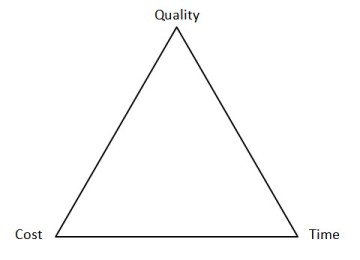
Figure 2: The Iron Triangle.

The relationship between the three constraints means that management staff end up having to make a choice between two out of the three of them; in other words, "Pick any two". Accordingly, one of the following is likely to occur:

ISO 9000

The ISO 9000 is family of standards that gives requirements for an organization's quality management system (QMS). It can be adopted to help ensure organisations meet the standards of customers and stakeholders whilst meeting the statutory and regulatory requirements of products. ISO 9000 is based on the following eight quality management principles:

  1. Customer focus
  2. Leadership
  3. Involvement of people
  4. Process approach
  5. System approach to management
  6. Continual improvement
  7. Factual approach to decision making
  8. Mutually beneficial supplier relationships

Global adoption of the ISO 9000 standard is growing annually - the number of global ISO certified organisations recorded in the world by the end of 2014 was 1,138,155, up from 409,421 by the end of 2000. The reason for the global adoption can be attributed to a number of the following:

  1. Creates a more efficient, effective operation
  2. Increases customer satisfaction and retention
  3. Reduces audits
  4. Enhances marketing
  5. Improves employee motivation, awareness, and morale
  6. Promotes international trade
  7. Increases profit
  8. Reduces waste and increases productivity
  9. Common tool for standardization http://www.emeraldinsight.com/doi/pdfplus/10.1108/17542730910995846 A range of Case Studies can be viewed to support the claims made.

Check Sheets

A Check Sheet is a form used to collect data in real time at the location where the data is generated. A simple example of a Check Sheet can be seen in Figure 3.

Figure 3: A simple example of a Check Sheet.

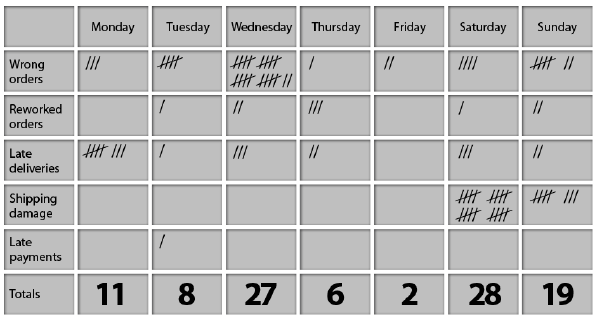
The pertinent advantages of utilising Check Sheets for gathering data are as follows:

  1. They are a quick, very easy and efficient means for recording desired information.
  2. Information gathered can be either qualitative or quantitative.

Check Sheets can generally be used to:

  1. Quantify defects by type, location, and cause (e.g. from a machine or worker).
  2. Keep track of the completion of steps in a multi-step procedure (i.e. be used as a checklist).
  3. Check the shape of the probability distribution of a process.

Pareto

The Pareto principle (also known as the 80 - 20 rule, the law of the vital few, and the principle of factor sparsity) states that, for many events, roughly 80% of the effects come from 20% of the causes. The term 80 - 20 is only a shorthand for the general principle at work. In individual cases, the distribution could just as well be, say, 80 - 10 or 80 - 30. There is no need for the two numbers to add up to the number 100, as they are measures of different things. A simple example of a pareto chart is presented in Figure 4.

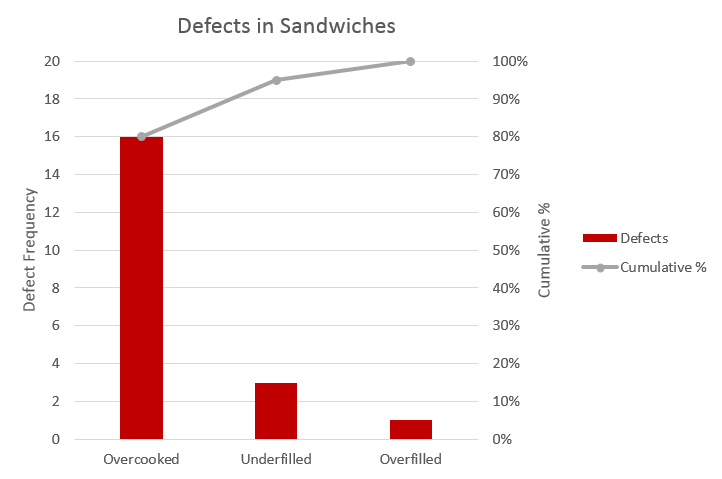
Figure 4: A simple example of a Pareto Chart.

If the two values sum to 100, this leads to a nice symmetry. For example, if 80% of effects come from the top 20% of sources, then the remaining 20% of effects come from the lower 80% of sources. This is called the "joint ratio", and can be used to measure the degree of imbalance. For example, a joint ratio of 96:4 is very imbalanced, 80:20 is significantly imbalanced, 70:30 is moderately imbalanced (Gini index: 40%), and 55:45 is just slightly imbalanced.

This principle is particularly prominent in the field of Software Engineering, as highlighted by the following examples:

Fishbone Ishikawa Diagrams

Ishikawa diagrams (also called fishbone diagrams) are causal diagrams that show the causes of a specific event. Common uses of the Ishikawa diagram are product design and quality defect prevention to identify potential factors causing an overall effect. Each cause or reason for imperfection is a source of variation. Causes are usually grouped into major categories to identify these sources of variation. The categories typically include:

A typical, simplistic example of an Ishikawa diagram is presented in Figure 5.

Figure 5: A simple example of a Fishbone diagram.

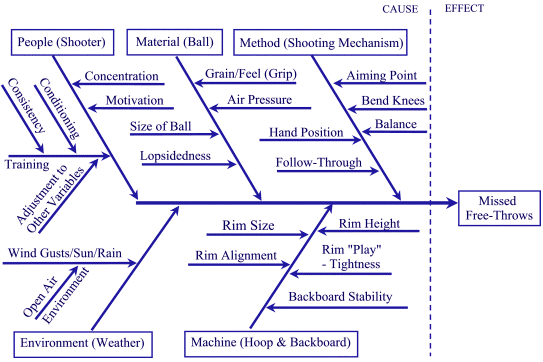
There have been identified topics for fishbone diagram cause classes in different areas of development. They are grouped into easily remembered sets, examples of which are presented below.

Cause Screening

Screening can be used to eliminate brainstorming and hypothesizing at the beginning of a project. The project team first makes non-invasive observations of the operation. They ignore everything in the middle, and only compare examples of the very best and very worst outputs, searching for consistent differences.

The guidelines are simple:

With this screening process, practitioners non-invasively observe and review data from the existing operation, and are usually able to separate the critical and non-critical factors more quickly than with the traditional trial-and-error approach.

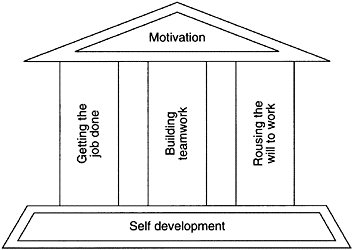
Teamwork

Teamwork should encompass the following concepts:

Teamwork is someting that requires training. Product owners should not delegate and control every aspect, as this can stifle teamwork and involvement. Constant improvement is the responsibility of managers. Most causes of low quality and productivity are due to issues at this level. An internal consultant can be hired to reslove teamwork issues.

Aspects related to Teamwork involve:

A diagram depicting the core principles of Teamwork can be seen in Figure 6.

Figure 6: Principles of Teamwork.

Multi-voting

Mutli-voting allows a group to narrow down a list of options into a manageable size for further consideration. It is useful for initiating a selection process after brainstorming. Multivoting is a group decision-making technique used to reduce a long list of items to a manageable number by means of a structured series of votes. The result is a short list identifying what is deemed important to the team.

Sometimes referred to as N/3 voting - for N options, each member of the group selects N/3 of the options as a means for partial-ordering the options by importance.

Multivoting Procedures:

Multivoting Rule of Thumb:

Size of Team Eliminate items with
5 or fewer 0, 1, or 2 votes
6 to 15 3 or fewer votes
more than 15 4 or fewer votes

Statistical Process Control

Statistical process control (SPC) is a method of quality control which uses statistical methods. SPC is applied in order to monitor and control a process. Monitoring and controlling the process ensures that it operates at its full potential. In this case, the process can make as many conforming products as possible while minimising waste. SPC can be applied to any process where the "conforming product" (product meeting specifications) output can be measured. Key tools used in SPC include control charts; a focus on continuous improvement; and the design of experiments. An example of a process where SPC is applied is manufacturing lines. It uses a process of physical inspection to separate good products from bad.

A key part of statistical process control is producing control charts (Figure 7) which can be used for visualising effects of eliminating process issues over time.

Figure 7: Quality Control Chart

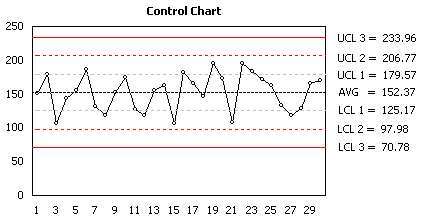
Objective analysis of variation

SPC must be practiced in 2 phases: The first phase is the initial establishment of the process, and the second phase is the regular production use of the process. In the second phase, a decision of the period to be examined must be made, depending upon the change in 4 - M conditions (Man, Machine, Material, Method) and wear rate of parts used in the manufacturing process (machine parts, jigs, and fixture).

Emphasis on early detection

An advantage of SPC over other methods of quality control, such as "inspection", is that it emphasizes early detection and prevention of problems, rather than the correction of problems after they have occurred.

Increasing rate of production

In addition to reducing waste, SPC can lead to a reduction in the time required to produce the product. SPC makes it less likely the finished product will need to be reworked upon completion.

Limitations

SPC is applied to reduce or eliminate process waste. This, in turn, eliminates the need for the process step of post-manufacture inspection. The success of SPC relies not only on the skill with which it is applied, but also on how suitable or amenable the process is to SPC. In some cases, it may be difficult to judge when the application of SPC is appropriate.

Taguchi

The Taguchi approach to Design of Experiments (DoE) necessitates the use of orthogonal arrays to implement fractional factorial experiments. Orthogonal in this sense essentially states that each control factor in the experiment is independent of each other and can thus be evaluated independently. The general approach to establishing Taguchi experiments is a three step process, as listed below:

  1. Identify the number of control factors required.
  2. Select the number of level settings for each control factor.
  3. Select an appropriate pre-defined Taguchi Array depending on the number of control factors and levels.

The three step process shall essentially define the number of experimental runs required. As an example, Figure 8 below represents a L9 orthogonal array which accounts for 4 control factors operating with 3 levels. It should be noted that there are an equal number of level 1, 2 and 3 settings across the nine experiments. In addition, there are an equal number of 1, 2 and 3 level settings for every other factor across all experimental runs.

Figure 8: An example of a Taguchi Array.

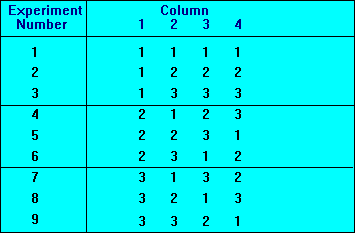
A more comprehensive list of available Taguchi Arrays can be consulted. The Taguchi process enables the addition of noise factors into the experiment. The noise is introduced into each run, with the resulting variation quanitfied as a comparable Signal to Noise Ratio (SNR). Control factor settings that minimise SNR are chosen to yield the most robust process possible. Noise added experiments are performed using duplicate Taguchi arrays to model the addition of the noise contol factors. An L9 Taguchi array with noise is presented in Figure 9 below.

Figure 9: An example of a Taguchi Array with noise.

The confirmation run is a crucial requirement when using Taguchi Arrays. Confirmation runs are needed in order to validate experimental success or identify problems with the experiment. These problems may potentially manifest themselves in the form of factors left out of the experiment, or interactions between the included control factors. The underlying advantages and limitations of Taguchi's approach to fractional factorial experiments are presented below.

Advantages:

Limitations:

Design of Experiments

Design of Experiments (DoE) represents a systematic method to determine the relationship between factors and their interactions to assess how these are affecting the output of that process. It is essentially an approach to determining 'cause and effect' relationships. The DoE method is used to maximize the information obtained from experimental data through very few trials or runs. Four approaches to DoE are listed below:

  1. Full factorial
  2. Fractional factorial
  3. Taguchi Methods
  4. RSM (Response Surface Methodology)

There are typically three components which comprise experimental design. These are detailed below. We take a simplistic example of a cake-baking process to contextualise the DoE approach:

Figure 10 presents the typical DoE approach to baking a cake, highlighting the factors, levels and typical responses.

Figure 10: An example of a DoE approach to baking a cake.

The rationale supporting the cake baking DoE approach is as follows:

The pertinent benefits of the DoE approach are as follows:

  1. Quick, economical and efficient method to identify most significant input factors.
  2. Simultaneous trials with multiple control factors instead of one variable at a time.
  3. Gives interaction effects of control factors.
  4. Fewer simulations required to get process insight.
  5. Factor effects can be easily measured.
  6. Explore relationship of response and control factors.
  7. Cheaper than reducing fabrication or simulation bottlenecks.

Software Process Improvement Tools

A Software process is defined as the system of all tasks and the supporting tools, standards, methods, and practices involved in the production and evolution of a software product. TQM tools, such as Cause & Effect Diagrams, Pareto Charts and Check Sheets can all be used to improve software processes.

One approach that can be used to improve a business' software process is the PDCA cycle - Plan, Do, Check and Act (The role of Software Process Improvement into Total Quality Management: an Industrial Experience, 2000). This approach can be split up into the following four steps:

References

Quiz

Which of the following characteristics best define the "Quality" of a product?

Given a threshold voltage of a MOS transistor has a nominal value of 0.5V, with tolerance +- 0.1V. The process mean is at the target value (0.5V), and the standard deviation for the process is 0.05V. What then is Cp?

For a market window of 24 months, if you aim to design a high-quality product, and you spend little capital on design and manufacture, how quickly should you expect the product to reach market?

Which of these characteristics do not describe check sheets?

What do the 80/20 refer to in the context of the Pareto rule?

What does a Fishbone-Ishikawa diagram aim to describe?

Which of the following is true about Cause Screening?

Which of the following is true about teamwork?

Which of the following would multi-voting be most useful for?

In the context of statistical process control, what do you need to do when a control chart value is outside a few standard deviations?

Which of the following are true about Taguchi process control?

When designing experiments using DoE methods, what is trying to be maximised?

Which of the following is not a step in the PDCA cycle?

Contact | Privacy Policy | Terms & Conditions | Copyright
Copyright © 2016 Burrito Rule